Counting Bits 라는 알고리즘을 풀게 되었다. 이 문제는 2020년 6월에 4일 동안 고민했으나 풀지 못했던 나에게 알고리즘의 좌절을 주었던 문제이다. 2021년 1월 10일날 이 문제를 푼건 나에게 여러모로 기쁜 의미가 있다
문제
Given a non negative integer number num. For every numbers i in the range 0 ≤ i ≤ num calculate the number of 1's in their binary representation and return them as an array.
어떤 양의 정수 n이 주어지면 0~n 까지 총 n+1 개의 배열을 만들어 이진수로 변환시 1의 개수를 반환하는 것이다.
사실 이 문제를 처음 접했을때 막막함은 이루 말할 수 없었다. 2진수로 바꾸어 1의 개수를 세자니 이 될 것이다. 그런데 follow up 을 보면 으로 풀라는 것이다.
심지어 c++ 에서 제공하는 2진수의 1을 count 하는 기능은 사용도 하지 말라고 한다
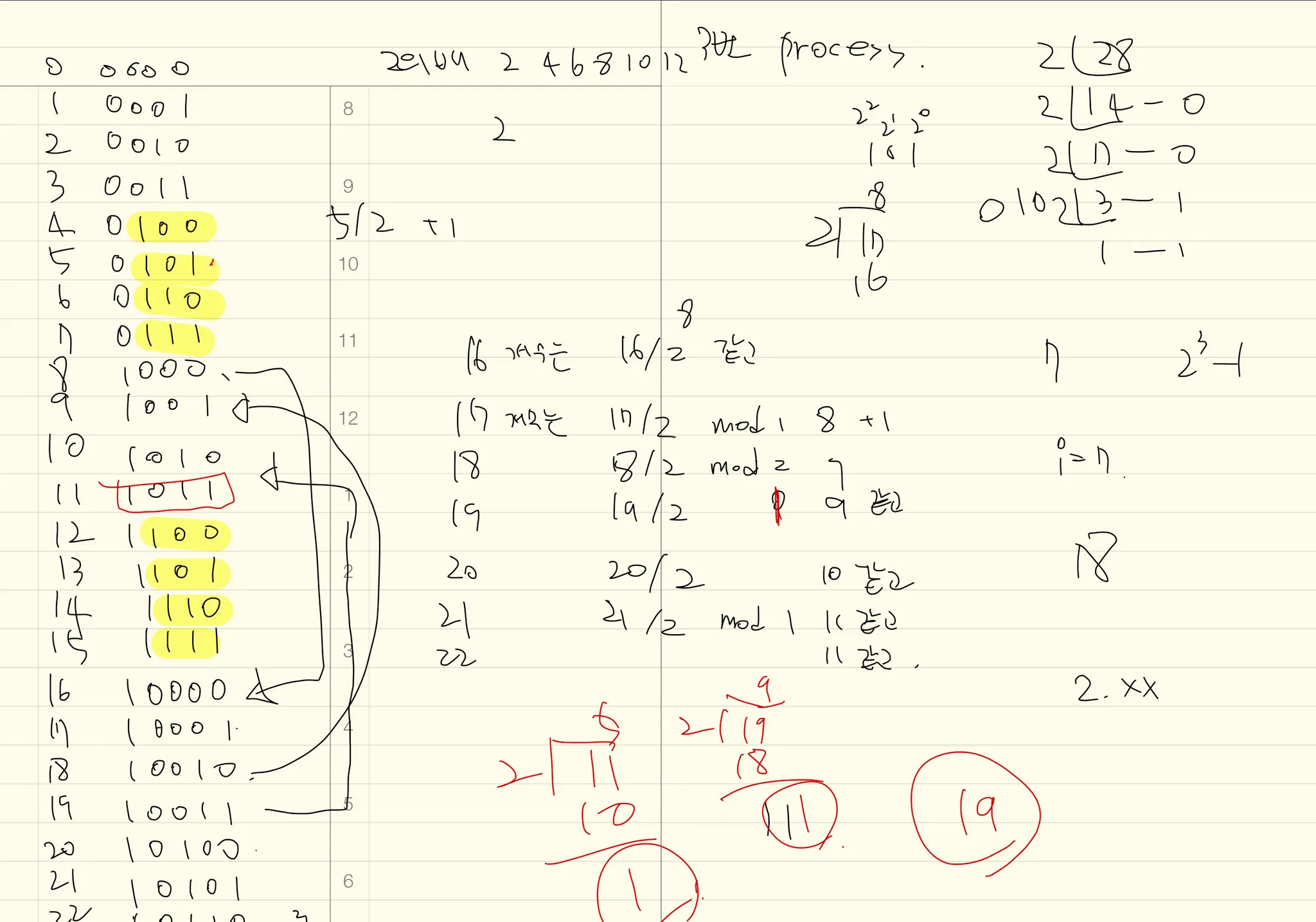
혼자 연습장에 쓰면서 접근한걸 보면 얼마나 멘붕이었는지 보여줄 수 있을것 같다.
하지만 여기서 특정한 숫자가 반복되어서 나타남을 확인할 수 있다.
그 반복 범위는 0~1, 2~3, 4~7, 8~15 와 같이 2의 제곱근의 범위에서 그 규칙성을 찾을 수 있다.
문제를 설명하기 위해 사용할 변수의 정의를 먼저 설명한다.
1.
num: param으로 입력 받은 변수
2.
result: 결과로 반환할 배열
재미있는 규칙은
•
을 만족한다면 1의 개수는 1이다.
•
인 경우 1의 개수는 n개 이다.
그래서 처음엔 두 개의 for 문을 작성해 을 맞추려고 했다.
for (int i = 0; i < Math.sqrt(num); i ++) {
int pow = (int) Math.pow(2, i);
result[pow] = 1;
result[pow-1] = i;
}
SQL
복사
그런데 발견된 규칙성은 다음과 같다
% 2 이유는 다음과 같다.
•
4 → 0100
•
5 → 0101
•
6 → 0110
•
7 → 0110
•
12 → 1100
•
13 → 1101
•
14 → 1110
•
15 → 1111
100, 101, 110, 111 이 반복된다. 그런데 더 큰 반복이 존재 하지 않을까? 라는 생각으로 범위를 넓혔다 이 반복을 찾아내고 그 반복을 캐싱하여 사용한다면 분명 요구사항에 맞는 로직을 작성할 수 있을 것이다.
•
0 → 0000
•
1 → 0001
•
2 → 0010
•
3 → 0011
•
4 → 0100
•
5 → 0101
•
6 → 0110
•
7 → 0110
•
8 → 1000
•
9 → 1001
•
10 → 1010
•
11 → 1011
•
12 → 1100
•
13 → 1101
•
14 → 1110
•
15 → 1111
1이 생기는 순서가 반복된다.
그렇다면 0~15의 이진수에서 발견된 패턴은 1만 더해 16 ~ 31까지 반복되지 않을까?
또한 0 ~ 31 에서 발견되는 패턴은 32 ~ 63 까지 반복되지 않을까?
그리고 이 문제가 DP 라고 생각되는건 i번째 element의 결과를 만들기 위해 i 보다 작은 위치 element 를 참조해야 한다. 그렇다면 DP 이고 점화식만 만들면 된다.
라는 점화식을 만족하게 된다.
class Solution {
public int[] countBits(int num) {
int[] result = new int[num+1];
for (int i = 0; i < num+1 ; i++) {
if (result[i] != 0) continue;
result[i] = result[i/2] + i % 2;
}
return result;
}
}
Java
복사
그런데 / 연산은 컴퓨터에서 상당히 느리다고 한다.
하지만 이것에 대해 잘 정리해 두었으니 면접을 대비해 한번 읽어보자
이 알고리즘에 대한 것도 정확히 살펴서 읽어볼 필요가 있겠다. (안읽어봤으니 물어보면 안댐!)
2로 나누는 것이라면
•
2를 나누기 보다 0.5 를 곱하는 방법이 컴퓨터에선 더 빠르다
•
2를 나누기 보다 비트를 우측 shift 하는 계산이 더 빠르다.
나눗셈 속도 > +, -, * > 비트연산
class Solution {
public int[] countBits(int num) {
int[] result = new int[num+1];
for (int i = 0; i < num+1 ; i++) {
result[i] = result[i>>1] + i & 1;
}
return result;
}
}
Java
복사
물론 큰 차이는 없다. 이것이 차이가 있다고 말할려면 위키 피디아에 있는 알고리즘을 설명해야 하는데 저 공부는 후에 하겠다.
비트 연산에 대해 더 자세히 알고싶다면
여기에서 다루었다.