ALU: Arithmetic Logic Unit: 산술 논리 장치
컴퓨터 안의 모든 계산은 ALU 라는 것으로 수행한다. 이 ALU 는 8가지 계산 방식을 제공하는데 다음과 같다.
우리의 컴퓨터는 이러한 ALU 가 포함되어 있으며, ALU의 모든 연산은 덧셈에 기반한다.
•
add: 더하기
•
add with carry: 더하기, 올림 ( 9 + 4 와 같은)
•
subtract: 빼기
•
subtract with borrow: 빼기, 내림 ( 3 - 7 과 같은)
•
negate: - → +, + → - 부호가 바뀜
•
increment: a ++
•
decrement: a —
•
pass through: 수정 없이 지나간다
Add, 더하기
여기서 보면 곱셈과 나눗셈이 없다.
덧셈은 그냥 덧셈이다
0 0 1 1
+ 0 0 1 0
-------
0 1 0 1
Plain Text
복사
Subtract, 빼기
보수를 구해 더한다
3-2 를 보수를 사용해 구하면 3 + 8 → 11 → 1 (올리는 숫자는 버린다) 이 된다.
0 0 1 1
- 0 0 1 0
-------
0 0 0 1
Plain Text
복사
0 0 1 1
+ 1 1 1 0
-------
0 0 0 1
Plain Text
복사
2의 보수를 더한다
1 complement, 1의 보수
NOT 연산을 취하면 된다
0 0 1 0
~ -------
1 1 0 1
Plain Text
복사
2 complement, 2의 보수
1의 보수에 + 1을 더한다
1 1 0 1
+ 0 0 0 1
--------
1 1 1 0
Plain Text
복사
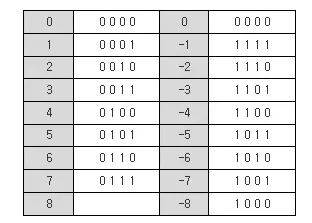
2의 보수 표, 2의 보수가 아니면 값이 틀어진다
Multiply, 곱셈
위의 ALU 를 보면 곱셈은 제공하지 않는다. 대신 특별한 방법을 사용하는데
3 * 2 라면 3을 2번 더하는 것이다
0 0 1 1
x 0 0 1 0
-------
0 1 1 0
Plain Text
복사
0 0 1 1
+ 0 0 1 1
-------
0 1 1 0
Plain Text
복사
나눗셈
핵심은 뺄셈이다. 앞서 언급했듯, 뺄셈엔 2의 보수를 구하는 연산이 계속 수행된다.
또한, 32 bit 머신이면 33번 반복하고
64bit 머신이면 65번 반복한다
remainder 에 dividend - divisor 를 저장하고 그 값이 0 이상인지, 아닌지 여부를 확인한다.
R := N
while R ≥ D do
R := R − D
end
return R
Plain Text
복사
문제는 뺄셈과 기존의 값을 가져오는 작업이다
1 1 0 1
/ 0 0 1 0
-------
Java
복사
13
/ 2
--
Java
복사
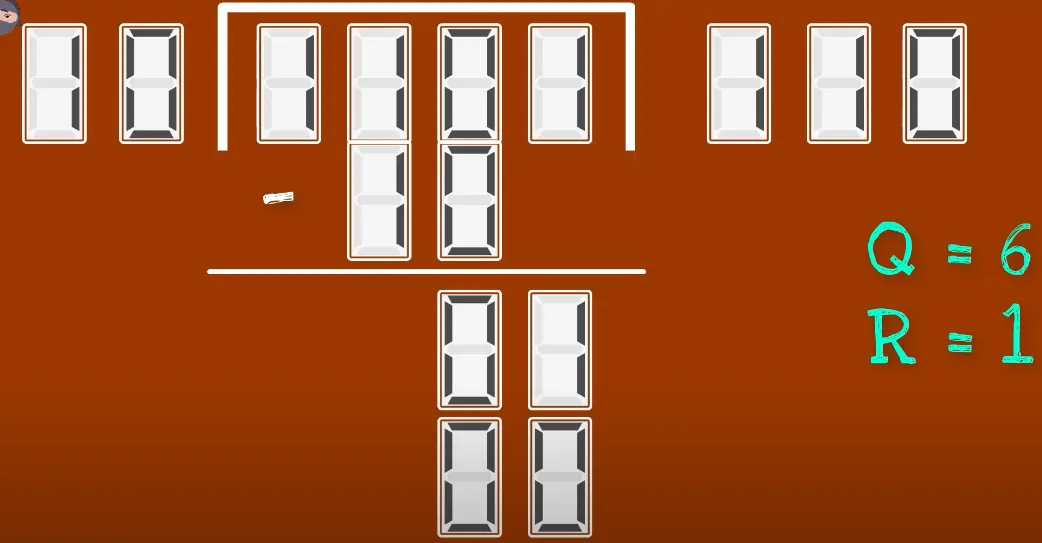
이 연산을 나누셈을 해보도록 한다
먼저 제일 앞에서 10 을 뺀다 - 가 된다 → 1
그리고 다시 - 이 된다 → 0
여기에선 를 뺄 수 없기 때문에 0 이 되고, 나머지는 1이 된다.
앞서 언급했듯, 빼기는 보수로 변환하는 작업이 필요하고 나누기는 반복 작업이 필요한데 반복 작업의 결과에 다시 빼기 작업을 한다
문제는 기계가 32bit 라면 33번, 64bit 라면 65번 반복이 필요하기 때문에 상당히 많은 연산이 수행된다는 점에서 나눗셈 연산은 필연적으로 느릴 수 밖에 없으니 되도록 bit 연산으로 문제를 해결하는 것이 좋다
33번, 65번 여러 연산을 반복한다면 shift 를 한번하는 비트연산에 비해 130배, 260배의 차이가 발생할 것이다.
이것과 관련된 알고리즘 문제가 있다. 이해했다면 한번 풀어보는것도 좋겠다