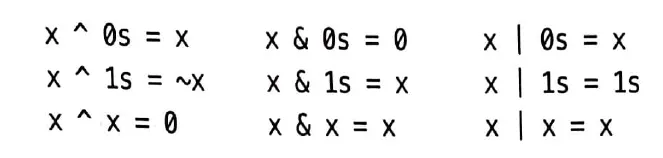코드를 최적화 할 때 유용하게 사용되는 기법중에 하나이다. 비트 연산은 손으로 풀 수 있을만큼 익숙할 필요가 있다. 알고리즘에서 Big O를 모두 최적화 했을때, 배열을 다뤄야 할 때 비트연산을 고민하면 더 좋은 성능을 기대할 수 있다.
이 컨텐츠는 코딩 인터뷰 완전분석 에서 정말 재미있게 읽었던 비트연산 부분을 발췌했다.
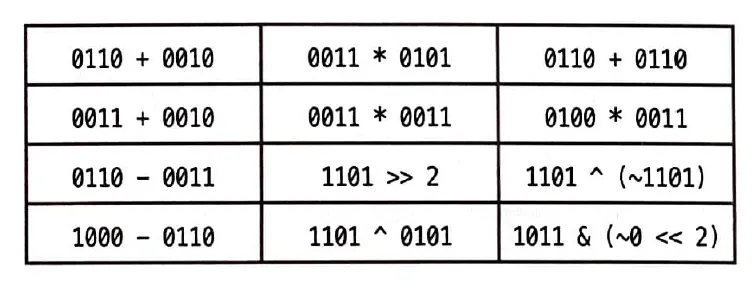
손으로 비트 조작 해보기
1.
아래 설명하는 트릭으로 풀기
2.
10진수로 변경하고 계산한 후 2진수로 변경한다.
정답
위 표에서 가장 오른쪽 열 4개만 살펴본다.
1.
0110 + 0110 은 0110 * 2 와 같고, 0110 을 왼쪽으로 한번 shift 하는것과 같다.
2.
0100 = 4, 0100 * 4 는 왼쪽으로 두번 shift 하는것과 같다.
•
0011 을 왼쪽으로 두 번 shift 하면 1100 이 된다.
3.
이 연산은 두개를 따로 생각해야 한다. a ^ (~a) 는 항상 1이 된다.
4.
~0 은 모두 1이 된다. (1111) 이 값은 and 연산하면 1000 이다.
비트 조작을 할 때 알아야 할 사실들과 트릭들
암기하기 보단 이해가 필요하다.
1s 는 1111 이고, 0s 는 0000 이다. 편의상 4자리 2진수라 가정한다
풀이
한 비트에서 일어나는 일이 다른 비트에 전혀 영향을 주지 않는다.
2의 보수와 음수
보수의 개념
컴퓨터는 정수를 저장할 때 2의 보수 형태로 저장한다. 양수는 문제가 없지만 음수는 절대값에 부호비트를 1로 셋팅한 뒤, 2의 보수를 취한 형태로 표현한다.
•
N비트 음수에 대한 2의 보수는 에 대한 보수와 같다.
◦
4비트로 표현된 정수 -3 으로 증명해보자
◦
4비트 중 하나는 부호를 표현한 값이다. → 3비트
◦
-3: 절대값 3의 = 8의 보수와 // -3의 2의 보수는 같다
▪
3은 8의 보수가 5이다. → 0101
▪
-3 은 1101 이다. (제일 앞에 캐리가 1이면 음수를 뜻한다)
◦
-K를 N비트 2진수로 표현하면 concat(1, ) 가 된다.
2의 보수는 1 → 0, 0 → 1로 전환하고(^1s) +1을 한다. 그리고 부호가 있으면 앞에 1을 붙인다.
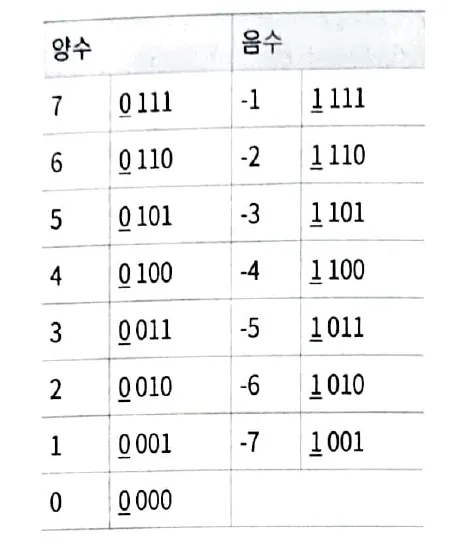
4비트 정수값을 위와 같이 표현한다.
왼쪽과 오른쪽의 절대값을 합치면 항상 8이 된다. 왜 그럴까?
산술 우측 시프트 vs 논리 우측 시프트
우측 시프트 연산은 두가지가 존재한다.
•
산술 우측 시프트(arithmetic right shift)
◦
2로 나눈것과 같다.
▪
가장 앞에 1을 계속 채워넣는다
▪
모두 1로 채워지면(1s) -1 이 된다.
◦
부호를 바꾸지 않는다
◦
>> 연산과 같다.
•
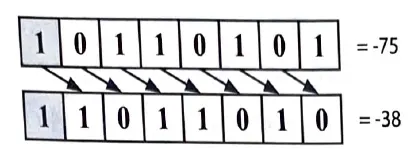
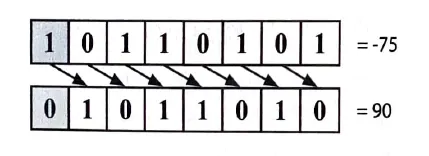
논리 우측 시프트(logical right shift)
◦
비트를 우측으로 옮긴 다음에 최상위 비트에 0을 넣는다
▪
회색 부분이 부호 비트를 나타낸다
◦
비트를 옮길 때 보이는 것 처럼 움직인다.
◦
>>> 연산과 같다.
◦
부호가 바뀐다.
◦
논리 shift 를 계속 사용하면 0이 된다.
기본적인 비트 조작: 비트값 확인 및 채워넣기
비트값 확인
1을 i 만큼 왼쪽으로 shift 하여 0001000 과 같이 만든다 → num과 & 연산을 하여 i 번째 위치 숫자를 제외하고 모두 삭제한다. → 이 값이 1이면 num 의 i 번째 비트는 1이 포함된 숫자이고, 0이면 num 의 i 번째는 0이 포함되었다.
boolean getBit(int num, int i) {
return ((num & (1 << i)) != 0);
}
Java
복사
비트값 채워넣기
특정 i 번째 위치에 1을 채워넣는다
1을 왼쪽으로 shift 하여 001000 과 같이 만들어 or 연산을 한다. 0인 곳은 기존의 값에 영향을 주지 못하고, i 번째 값은
int setBit(int num, int i) {
return num | (1 << i);
}
Java
복사
비트값 삭제하기
특정 bit 만 삭제한다.
getBit 를 반대로 했다. 001000 을 ~ 연산자를 사용해 110111 으로 만들어 and 연산을 하여 특정 위치의 bit 를 제거한다
int clearBit(int num, int i) {
int mask = ~(1 << i);
return num & mask;
}
Java
복사
최상위 비트에서 i번째 비트까지 모두 삭제하기
i 번째 bit 를 셋팅하고 -1 을 하면 최상위 부터 i 번째 까지 0으로 채워지고, 그 뒤는 1로 채워진다
이 값을 num에 & 연산을 하면 앞을 0 때문에 0으로 지워지고 그 뒤는 모두 1 때문에 그대로 남아 있는다.
int clearBitsFromHead(int num, int i) {
int mask = (1 << i) - 1;
return num & mask;
}
Java
복사
0 ~ i 까지의 bit 를 전부 삭제한다.
비트가 모두 1 이면 10진수로 -1 이 된다. -1에 i+1 만큼 시프트 시킨 후 그 값을 & 연산한다.
int clearBitFromTail(int num, int i) {
int mask = (-1 << (i+1));
return num * mask;
}
Java
복사
i번째 bit 를 v로 변경하기
int updateBit(int num, int i, boolean bitIs1) {
int value = bitIs1 ? 1 : 0;
int mask = ~(1 << 1);
return (num & mask) | (value << i);
}
Java
복사
면접 문제
5.1 삽입
두개의 32비트 수 N, M 이 주어지고, 비트 위치 i, j가 주어졌을 때, M을 N에 삽입하는 method를 구현하라.
•
M은 N의 j번째 비트에서 시작하여 i번째 비트에서 끝난다.
•
j번째 비트에서 i번째 비트까지에는 M을 담기 충분한 공간이 있다고 가정한다.
•
입력 N = 1000000000, M = 10011, i = 2, J =6
•
출력 N = 10001001100
public int bitInsert(int m, int n, int i, int j) {
m = bitDeleteFrom(m, j, i);
n = leftBitShift(n, i);
System.out.println("m: " + Integer.toBinaryString(m) + ", n: " + Integer.toBinaryString(n)
+ ", m + n: " + Integer.toBinaryString(m+n));
return m + n;
}
private int bitDeleteFrom(int num, int start, int end) {
int mask = (1 << (start + 1)) - 1;
mask = mask >> end;
mask = mask << end;
return num & ~mask;
}
private int leftBitShift(int num, int j) {
return num << j;
}
Java
복사
5.3 비트 뒤집기
어떤 정수가 주어졌을 때 이 정수의 비트 하나를 0에서 1로 바꿀 수 있다. 이때 1이 연속으로 나올 수 있는 가장 긴 길이를 구하는 코드를 작성하라.
private String convert1bit(int data) {
String[] d = String.valueOf(data).split("0");
int max = 0;
int maxIndex = 0;
for (int i = 0; i < d.length; i++) {
if (d[i].length() > max) {
max = d[i].length();
maxIndex = i;
}
}
String result = "";
if (maxIndex < d.length-1 && d[maxIndex+1] != "") {
result = d[maxIndex] + "1" + d[maxIndex+1];
}
if (maxIndex > 0 && d[maxIndex-1] != "") {
String re = d[maxIndex-1] + "1" + d[maxIndex];
if (result.length() < re.length()) {
return re;
}
}
return result;
}
Integer.toBinaryString(1024);
Java
복사
2진수를 문자로 바꾸어 split("0") 하고, 앞 뒤 문자열을 비교한다
5.5 디버거
다음 코드가 하는 일을 설명하라.
((n & (n-1)) == 0)
SQL
복사
n 은 2의 거듭제곱인가?
1000
& 0111 (= 1000 - 0001)
----------------------
0000 -> true
Java
복사
1100
& 1011 (= 1100 - 0001)
-----------------------
1000 -> false
Java
복사