2 point 전략으로 푸는 문제중 너무 신박한 접근을 발견하여 정리를 해본다.
내가 푼 방식
class Solution {
public int[] twoSum(int[] numbers, int target) {
for (int i = 0; i < numbers.length; i ++) {
int num = target - numbers[i];
if (i > 0 && numbers[i-1] == numbers[i]) {
continue;
}
for (int j = i+1; j < numbers.length; j ++) {
if (num == numbers[j]) {
return new int[] {i+1, j+1};
}
}
}
throw new IllegalArgumentException();
}
}
Java
복사
나의 접근
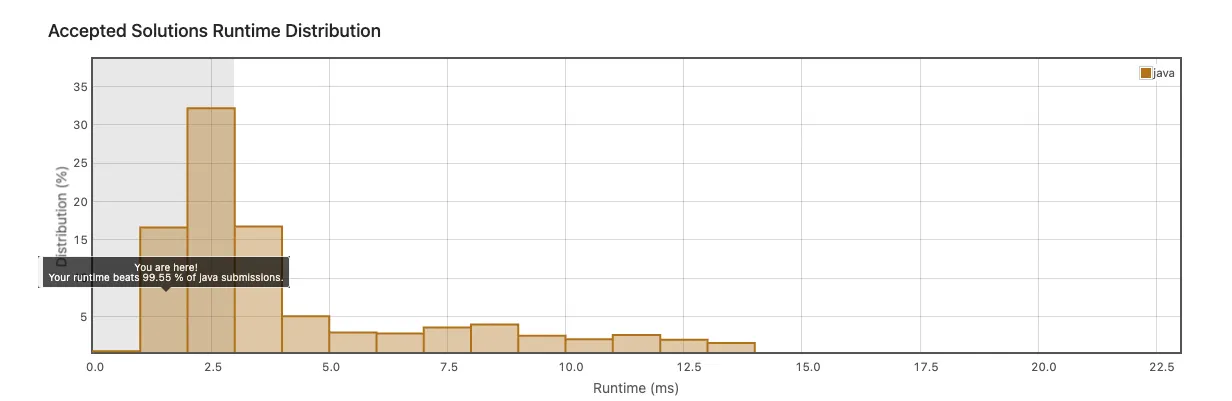
2중 for 문을 사용하였지만 Runtime을 비교해봤을 때 그리 느리지 않은 속도가 나타난다.
이유는 Time Limit exception 을 경험하면서 어떻게 캐싱과 같이 이전에 같은 결과가 나오는 경우 inner-for 를 수행하지 않을까? 라고 문제를 특정했기 때문이다.
You are here! Your runtime beats 99.55 % of java submissions
해결 방법은 i가 0보다 클때, i-1 에서 경험한 결과에 내가 찾는 경우(target을 완성하는 케이스)가 없다면, i 에서도 없기 때문에 continue 로 넘어갔다.
if (i > 0 && numbers[i-1] == numbers[i]) {
continue;
}
Java
복사
0 보다 커야 하는 이유는 첫 번째는 이전 케이스가 없기 때문이다.
신박한 풀이
class Solution {
public int[] twoSum(int[] numbers, int target) {
int start = 0, end = numbers.length - 1;
while(start <= end){
int mid = start + (end - start) / 2;
int sum = numbers[start] + numbers[end];
if(sum == target)
return new int[]{start + 1, end + 1};
if(target < sum){
if(target <= numbers[start] + numbers[mid])
end = mid;
else end--;
}
else{
if(target > numbers[mid] + numbers[end])
start = mid;
else start++;
}
}
return new int[]{end + 1, start + 1};
}
}
Java
복사
역시 문제를 잘 읽어야 한다.
문제에 보면 already sorted in non-decreasing order 와 같은 힌트가 포함되어 있다.
Non-decreasing order 란 오름차순이고(and) 같은 값이 올 수 있다는 뜻이다.
즉, 배열의 왼쪽 끝을 start, 오른쪽 끝을 end 로 명명 했을 때 3가지 케이스가 있다.
(1) 은 코드에서 을 정의한 방법이다.
(2)가 만족된다면 start 는 더 오른쪽으로 와야 한다.
(3)이 만족된다면 end 는 더 왼쪽으로 와야 한다.
(4)를 만족하면 우리가 찾는 정답이다.
결론
(2)~(3) 과 같이 판단할 수 있는 이유는 Non-decreasing order 이기 때문이다.
단조 증가 및 같은 값이 index 가 증가할 수록 array 에 있음을 보장하는 non-decreaseing order의 특징으로 볼 때, 다음 target 과 동일한 sum 의 위치는 추론이 가능하기 때문이다.