요즘 Bit 연산의 매력에 빠져들었는데 이 기회에 2의 보수가 뭔지 왜 필요하게 된 것인지 한번 정리해보려고 한다. 2의 보수를 알려면 1의 보수부터 정리해야 한다.
그 전에 우리끼리 한가지 함수를 만들었으면 한다.
fun inverse(number: Int): Int
Kotlin
복사
이 함수는 어떠한 숫자를 받으면 2진수로 반전 시킨다고 가정하자. 내부 구현은 논의하지 않겠다.
예를들어 1101 이 입력되면 출력은 0010 으로 반환된다.
보수
사전적 정의는 네이버 국어사전에서 가져왔다.
수학 각 자리의 숫자의 합이 어느 일정한 수가 되게 하는 수. 예를 들어 10의 7에 대한 보수는 3이다.
1의 보수
•
1의 보수는 위의 정의로 파악하면 다소 어렵다.
•
일단 비트를 반전 시킨다고 이해하면 좋다.
•
임의의 숫자 n 이 있을때 1의 보수는 위에서 정의한 함수 inverse(n) 의 결과가 1의 보수이다.
2의 보수
•
1의 보수에 + 1을 더하면 나온값이다.
왜 컴퓨터는 2의 보수를 사용할까?
개념 설명
•
컴퓨터에서 2진수는 00000101 은 십진수로 5 이다.
•
컴퓨터에서 -5는 10000101 로 앞에 1을 붙이면 -5가 된다.
◦
가장 첫 번째 자리를 sign bit 라 한다.
•
8자리를 사용하니 8 bit 숫자이다.
1의 보수
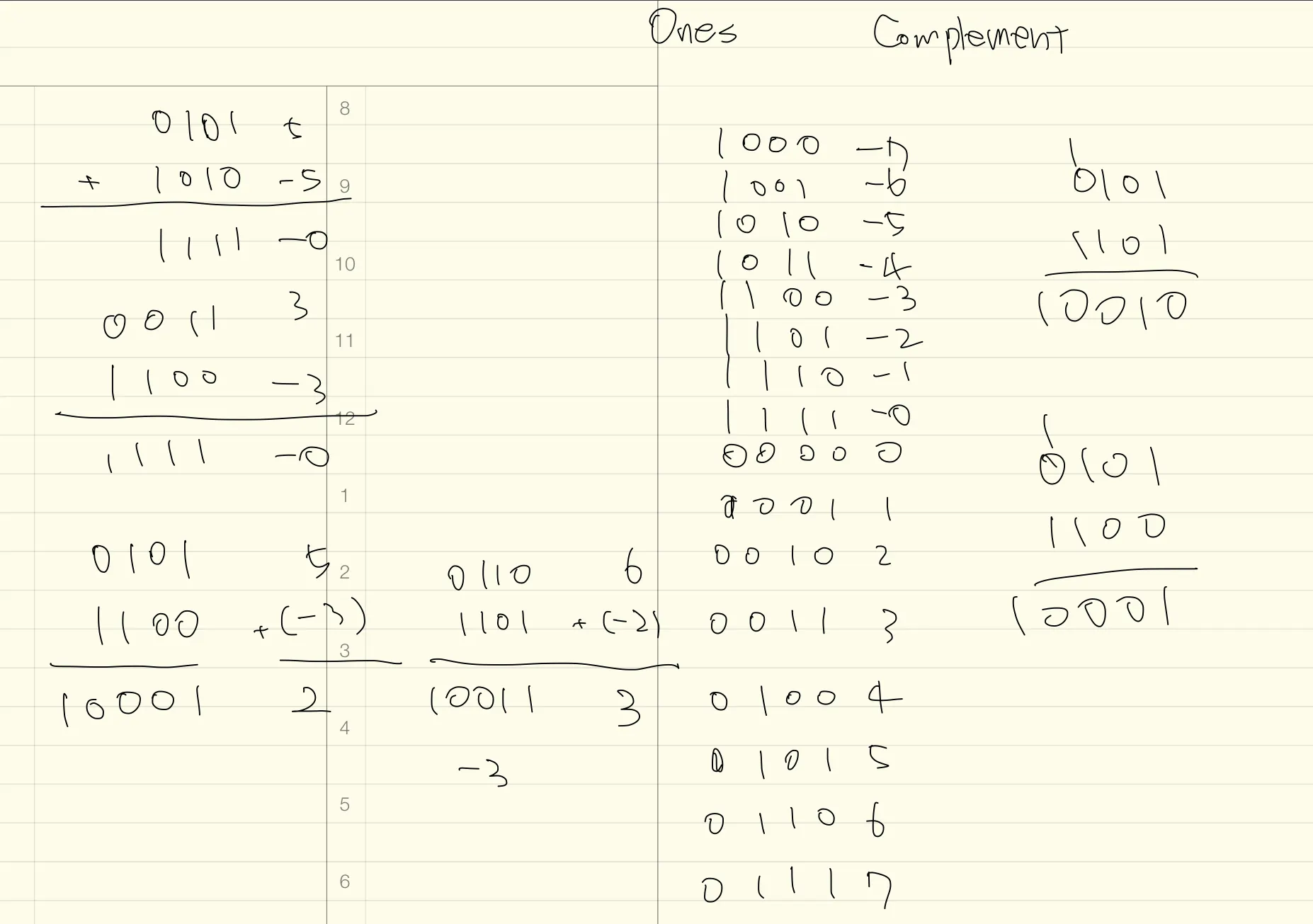
1의 보수는 다음과 같다. 편리한 설명을 위해 4bit로 작성한다.
1.
-1 은 inverse(1) 이다.
2.
-0 이 존재한다.
의 결과는 어떻게 될까?
이고 이 값은 이다.
의 결과는 어떻게 될까?
1이 carriage bit 가 되어 5bit 값이 나온다.
하지만, 4bit 만 연산하기로 했기 때문에 앞의 1은 제외한다.
2진수 연산을 그대로 10진수로 옮기면 위와 같다.
실제로 5-2 는 3이지만, 1의 보수로 연산하면 2이다.
의 결과는 어떻게 될까?
동일하게 carriage bit 이 존재하지만 4bit 이므로 무시한다.
는 1의 보수에서 십진수로 1을 의미한다. 실제로는 2 이지만
1의 보수의 연산
•
5 + (-5) = -0
•
5 + (-2) = 2
•
5 + (-3) = 1
각각 1을 더하면 -0 을 제외하고는 실제 10진수의 연산 결과와 같다.
•
5 + (-5) = -0 + 1 = 1 (very close, not same)
•
5 + (-2) = 2 + 1 = 3 (same)
•
5 + (-3) = 1 + 1 = 2 (same)
2의 보수
1.
-0은 존재하지 않는다.
2.
1의 보수 + 1
의 결과는 어떻게 될까?
이진수로 이고 이 10진수 값은 이다.
의 결과는 어떻게 될까?
1이 carriage bit 가 되어 5bit 값이 나온다.
하지만, 4bit 만 연산하기로 했기 때문에 앞의 1은 제외한다.
는 10진수로 3이다.
5-3 은 의심의 여지없이 3이다.
의 결과는 어떻게 될까?
1이 carriage bit 가 되어 5bit 값이 나온다.
하지만, 4bit 만 연산하기로 했기 때문에 앞의 1은 제외한다.
는 십진수로 계산하면 2 이다.
5-3은 2이다.
이렇게 계산해보면 오차 없이 가장 정확한 연산이 2의 보수가 된다. 따라서 컴퓨터는 양수, 음수의 연산의 오차를 제거하기 위해 2의 보수를 사용하는 것이 더욱 타당해진다.
함께 읽어보면 좋은 글