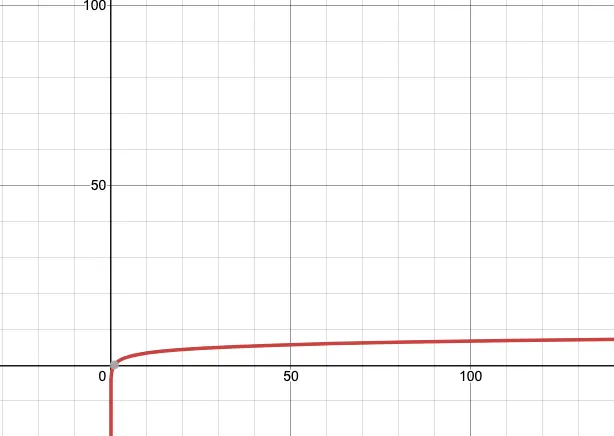
Binary Search 는 왜 으로 시간 복잡도를 설명할까? 시간, 공간 복잡도는 이전에도 다뤄본적이 있지만, 수학적으로 증명할 필요가 있다 여겨 살펴보게 되었다.
이전에 작성했던 글은 Recursive 인데 Big O table 이 포함되어 있다
참조한 대표적인 contents 는 youtube와 geeksforgeek 이다
binary search 의 선제 조건은 입력받은 배열이 sorting 되어 있다는 점이다.
fun binarySearch(arr: Array<Int>, findValue: Int, start: Int, end: Int): Int {
val middleIndex = (start + end) shr 1
return if (arr[middleIndex] == findValue) {
arr[middleIndex]
} else if (start == end) {
-1
} else if (arr[middleIndex] > findValue) {
binarySearch(arr, findValue, start, middleIndex - 1)
} else {
binarySearch(arr, findValue, middleIndex + 1, end)
}
}
Kotlin
복사
이러한 binary search 함수를 만들었다 recursive 로 구현하였고 우리가 아는 binary search 알고리즘이다
주어진 배열은 다음과 같다
[3, 6, 9, 13, 17, 24, 39, 57, 73, 92]
Kotlin
복사
여기서 우리가 할 일은 24를 찾는 것이다.
Iteration 1
•
arr: [3, 6, 9, 13, 17, 24, 39, 57, 73, 92]
•
middleIndex 를 찾아낸다 여기서는 4가 된다
•
index 4의 value 는 24 이다.
•
길이는 10이다
Iteration 2
•
arr: [24, 39, 57, 73, 92]
•
middleIndex: 7
•
value: 57
•
length: 5
Iteration 3
•
arr: [24, 39]
•
middleIndex: 0
•
value: 24
•
length: 2
•
MATCHED!
24를 찾을 경우의 수
Iteration 1
Iteration 2
Iteration3
따라서 k 번 iteration을 해야한다면 다음과 같은 수식으로 귀결된다
를 구하기 위해서 다음과 같이 정의할 수 있다
이므로 k는 다음과 같다
계차수열의 합 공식인줄 알았는데, 그냥 공비수열이었음.....
수열간의 관계