알고리즘을 풀다가 inorder 로 tree 를 저장하라는데 inorder 가 뭔지 알아둬야 할거 같아 정리해둔다.
What is inorder?
이해를 위한 test case.
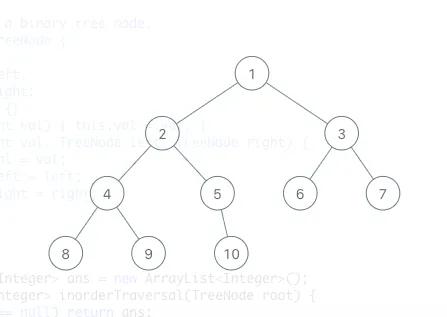
문제를 위해 다소 depth 가 있는 tree 를 다음과 같이 sample 을 정의하자.
[1,2,3,4,5,6,7,8,9,null,10]
Java
복사
이해를 위해 만들어본 tree
위 tree 의 결과
그렇다면 inorder 로 순회할 경우 나오는 list 는 다음과 같다.
Sample 의 결과
[8,4,9,2,5,10,1,6,3,7]
Java
복사
주어진 문제의 정답
Sample을 통해 확인한 inorder
주어진 답으로 봤을때 1, 2, 3 의 순서로 순회해야 8 → 4 → 9 → 2 →5 순서로 접근한다.
즉, 가장 왼쪽으로 도착해서 node 의 값을 저장하고 그 node 의 부모, 그리고 오른쪽 자식을 저장해야 한다.
알고리즘을 많이 푼 사람들은 이런 접근 순서별로 code 를 외워 두기도 한다.
해결 코드
class Solution {
private List<Integer> ans = new ArrayList<Integer>();
public List<Integer> inorderTraversal(TreeNode root) {
if (root == null) return ans;
inorder(root);
return ans;
}
private void inorder(TreeNode root) {
if (root==null) return;
inorder(root.left);
ans.add(root.val);
inorder(root.right);
}
}
Java
복사
해결방안
이 정도 코드는 DFS 를 다루다 보면 거의 반사적으로 나오는 코드이다.
그래서 어떻게 동작하는 것일까? 늘 재귀호출이 머리속에서 잘 그려지지 않았는데 이번 기회에 정확히 그려보자.
재귀호출
코드가 실제로 동작하는 것을 확인하기 위해 다음과 같이 log 를 추가해봤다.
inorder 함수에 진입하는 시점에 왼쪽 자식으로 진입한 것인지, 오른쪽 자식으로 진입한 것인지 확인하기 위한 로그를 추가했고 그 결과이다.
private void inorder(TreeNode root, Boolean left) {
if (root==null) return;
System.out.println("left " + left + ", add: "+root.val);
inorder(root.left, true);
ans.add(root.val);
inorder(root.right, false);
}
Java
복사
console 에 찍어보기 위해 추가한 코드
left null, val: 1
left true, val: 2
left true, val: 4
left true, val: 8
left false, val: 9
left false, val: 5
left false, val: 10
left false, val: 3
left true, val: 6
left false, val: 7
Java
복사
변경된 코드로 console 에 찍힌 결과
val 은 알겠는데, List 에 add 하는 시점에 한번 더 로그를 추가해보자
left null, val: 1
left true, val: 2
left true, val: 4
left true, val: 8
save: 8
save: 4
left false, val: 9
save: 9
save: 2
left false, val: 5
save: 5
left false, val: 10
save: 10
save: 1
left false, val: 3
left true, val: 6
save: 6
save: 3
left false, val: 7
save: 7
Java
복사
[8,4,9,2,5,10,1,6,3,7] 순서대로 저장이 일어남을 볼 수 있다.
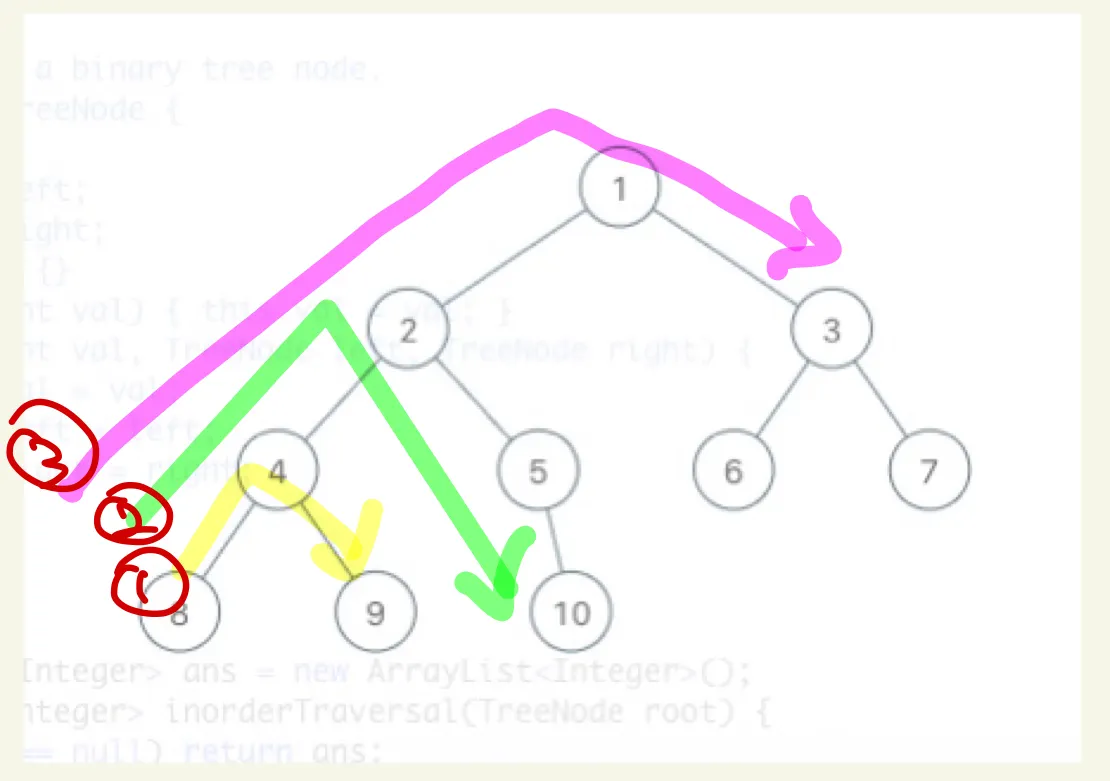
재귀호출을 더 잘 이해하기 위해 한 node 한 node 를 따라가 보자.
•
root 에 접근하고 왼쪽 가장 하단 leaf node 로 이동한다.
◦
1 → 2 → 4 → 8 이동
•
왼쪽 하단 leaf node 에 도착하면 값(8)을 저장한다.
◦
4번 node 의 left child 이다.
◦
놓칠 수 있지만, 8번이 저장된 node 에서도 left, right 의 방문이 있었다.
◦
다만 null 이기 때문에 바로 함수가 return 된 것이다.
•
add 이후 (4번의 left child) 이기 때문에 4번이 저장된다.
•
Right child 인 9번이 저장된 node 에 진입한다.
•
9번 node 의 left child 에 진입한다.
•
null 이기 때문에 함수가 종료된다.
•
9번을 저장한다.
•
Right child 에 방문하지만, 역시 null 이기 때문에 함수가 종료된다.
•
4번 node 의 right child 를 방문하는 함수 호출이 종료된다.
•
2번 node 에서 left child 로 방문하는 함수가 종료되었다.
•
2번을 List 에 저장한다.
•
2번의 right child 로 방문한다.
•
5번의 left child 로 접근하지만 null 이기 때문에 함수는 종료된다.
•
5번 저장
•
5번의 right child 인 10으로 이동한다.
•
10번 node 의 left 에 방문하지만 null 이므로 함수는 종료된다.
•
10번을 List 에 저장한다.
•
10번의 right child 로 이동하지만, null 이므로 함수는 종료된다.
•
5번의 right 방문 함수 종료
•
2번의 right 방문 함수 종료
•
1번의 left 방문 함수 종료
•
1번을 저장한다.
•
1번의 right child 로 진입한다.
•
3번의 left child 를 방문한다.
•
6번의 left child 를 방문하지만, null 이므로 함수는 종료된다.
•
6번을 저장한다.
•
6번의 right child 를 방문하지만, null 이므로 함수는 종료된다.
•
6번 left child 방문 함수 종료, 3번 복귀
•
3번을 List 에 저장한다.
•
3번의 right child 진입
•
7번의 left child 에 진입 하였으나, null 이므로 함수는 종료된다.
•
7번을 List 에 저장한다.
•
7번의 right child 에 진입 하였으나, null 이므로 함수는 종료된다.
•
3번의 right child 진입 함수 종료
•
1번의 right child 진입 함수 종료
Inorder 의 정의
•
이렇게 left, root, right 방식으로 접근하는 것을 Inorder, 중위 순회 라고 한다.
•
함수는 계속해서 left child 로 접근하기 때문에 가장 먼저 저장되는 것이 left 의 leaf node 이다.
그런데 Inorder 에 접근하는 것은 위와 같이 DFS 와 함께 stack 을 사용하는 방법도 있다고 한다.